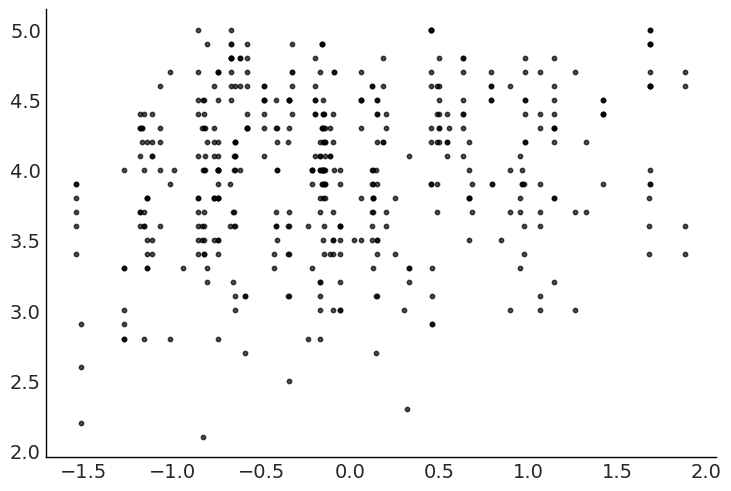
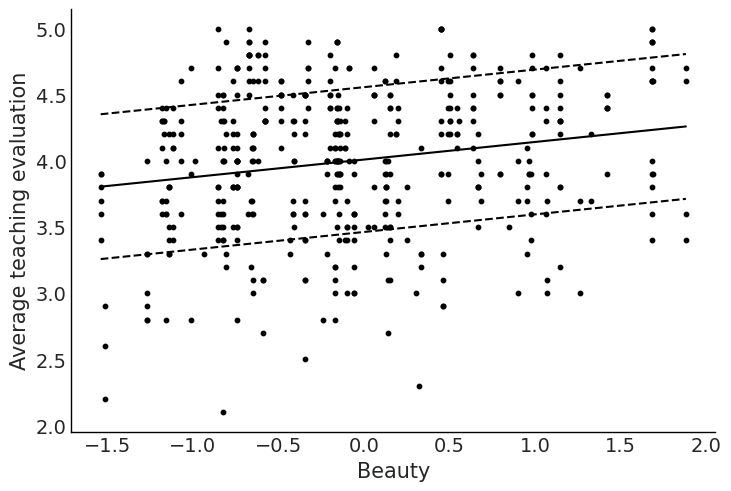
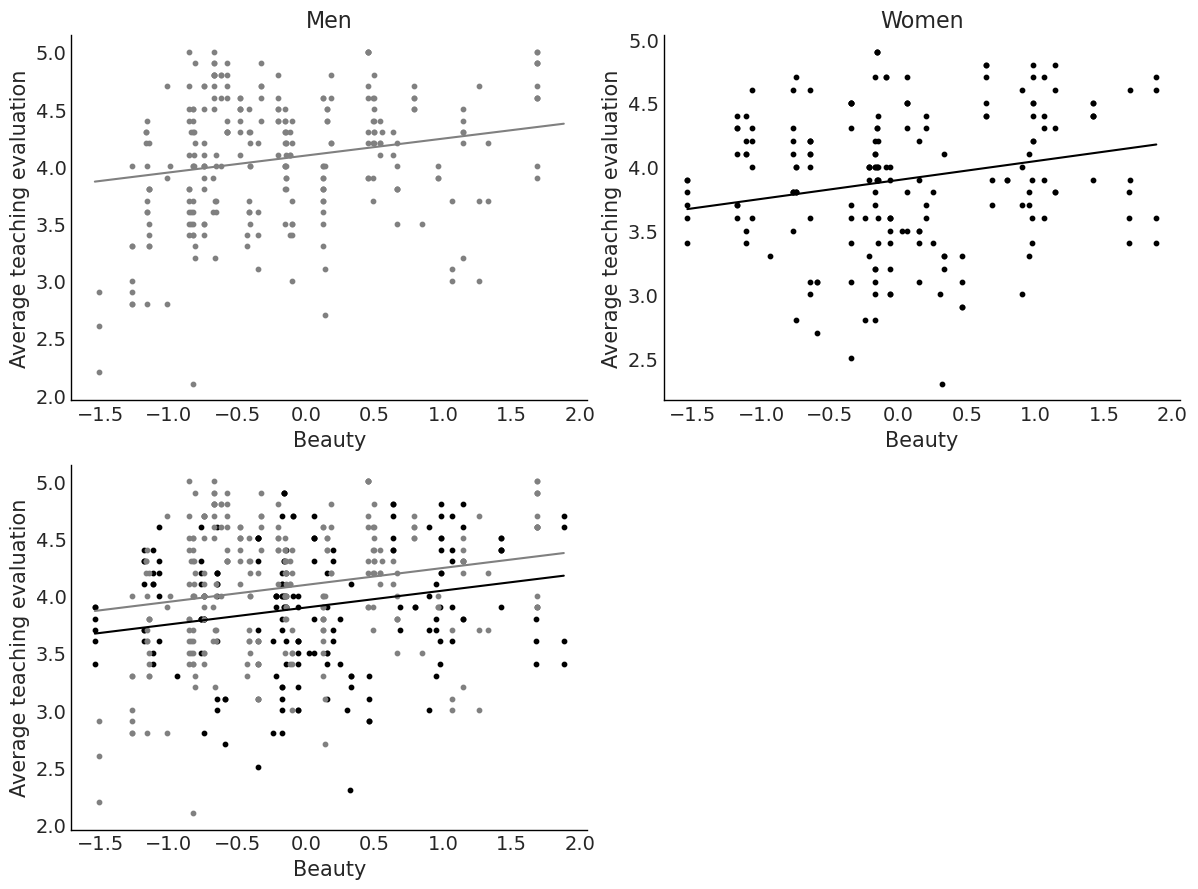
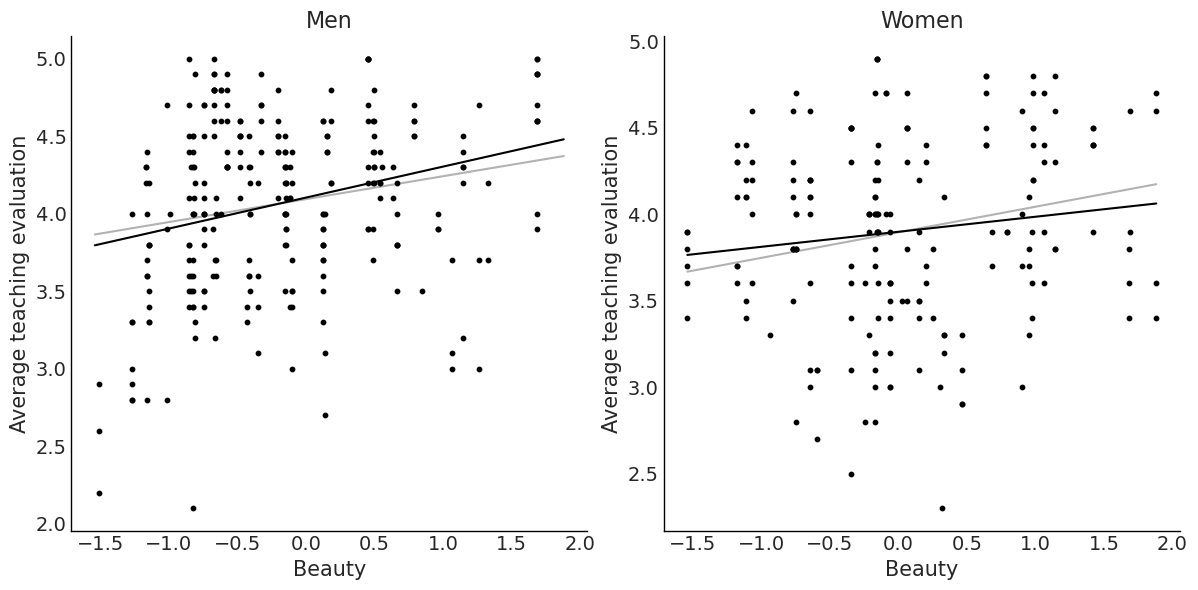
= az.summary(idata_2, kind= "stats" )["mean" ]= np.linspace(beauty["beauty" ].min (), beauty["beauty" ].max (), 10 )= stats_2["Intercept" ] + stats_2["beauty" ] * x= stats_2["Intercept" ] + stats_2["female" ] + stats_2["beauty" ] * x= plt.subplots(2 , 2 , figsize= (12 , 9 ))# Men "beauty" , "eval" , data= beauty.query("female == 0" ), color= "grey" , s= 10 )"Men" )"Beauty" )"Average teaching evaluation" )= "grey" )# Women "beauty" , "eval" , data= beauty.query("female == 1" ), color= "black" , s= 10 )"Women" )"Beauty" )"Average teaching evaluation" )= "black" )# Both sexes "beauty" , "eval" , data= beauty.query("female == 1" ), color= "black" , s= 10 )"beauty" , "eval" , data= beauty.query("female == 0" ), color= "grey" , s= 10 )"Beauty" )"Average teaching evaluation" )= "black" )= "grey" );